この記事は「いのべこ夏休みアドベントカレンダー2020」の4日目の記事です。本記事の掲載内容は私自身の見解であり、所属する組織を代表するものではありません(お約束)。
TOP500とLinpack
2020年6月、理化学研究所と富士通が共同開発しているスーパーコンピュータ「富岳」がISC2020で発表された世界ランキングで4冠を獲得したニュースは、大変話題になりました。今回獲得した4冠というのは、それぞれ下記のベンチマークについて最高性能を達成したことになります。
- TOP500:大規模連立一次方程式を解くLINPACKライブラリの実行性能を測定。密行列演算に対するベンチマーク。
- HPCG:共役勾配法による連立一次方程式解法の演算性能を測定する。疎行列演算に対するベンチマーク。
- HPL-AI:倍精度浮動小数点を扱うHPL/HPCGに対し、AI学習で多用される単精度や半精度演算の処理性能に対するベンチマーク。
- Graph500:1秒間のグラフ構造の枝を辿る操作回数を測定する。グラフを扱う性能のベンチマーク。
このうちTOP500で使われているベンチマークは「HPL」といい、1979年に初期のスーパーコンピュータに提供されたLINPACKライブラリ(実装はFORTRAN言語)を起源とし、アルゴリズムが改善されたHPLinpackをC言語で実装したものです。HPLの「HP」は「Highly Parallel Computing」を意味し、行列サイズをベンチマーク対象のコンピュータの最高性能を引き出せる任意の値に可変できることから、性能がどんどん上昇するスパコンのベンチマークとして、今も使われています。
WindowsノートPCでLinpackベンチマークを試す
HPLはスーパーコンピュータでなくとも、パソコンで試せるような実装が存在しますので、私のノートPCを使って実際に動作させてみたいと思います。パソコンでも試せる実装を調べてみると、下記の2つがありました。
- Intel Math Kernel Library (MKL) Benchmark:Intelによる実装で、Windows/Mac/Linux版がある
- lu2:神戸大学大学院の牧野淳一郎教授による実装で、Linux版のみ
なお、残念ながら後者のlu2はWSL2+Ubuntu環境でコンパイルまで通っているもののエラーが解消できず、実行させられませんでした。従って今回は前者のみテストします。
今回使ったPCのスペックは下記です。CPUはIntelでなくAMDのRyzen mobile。これがちょっとした混乱を招きます。

- 機種:ASUS ROG Zephyrus G14(GA401IU-R7G1660TWL)
- CPU:AMD Ryzen 7 4800HS(8コア16スレッド、クロック 2.9-4.2GHz、L3キャッシュ 8MB、TDP 35W)
- メモリ:16GB(DDR4-3200、デュアルチャネル動作)
- OS:Windows 10 Home May 2020 Update
Intel MKL Benchmarkの実行
Intel公式のベンチマークで、ここから入手可能。Windows/Mac/Linuxと各種OS版が揃ってるけど、なんとCPU-IDをチェックしており、「Intelハイッテル」PCでしか動作しません。ぐぬぬ。
しかしこのベンチマークをもとにIntel以外のCPUでも実行できるようにしたプログラム「LinpackXtreme」があります。Intel MKL Benchmarks の2018.3.011版ベースというこのプログラムは、32bit版と64bit版の実行ファイルが同梱されています。しかし64bit版は動作しなかったため、今回は32bit版のみ動作させました。使用メモリ量の大小を3段階に変えて実行ができますが最大で1.5GBにとどまっています。そのためか結果としては大差なく、110~115GFlopsという結果が出ました。
実行結果(Quick 256MB Benchmark)
Maximum memory requested that can be used=200104096, at the size=5000
=================== Timing linear equation system solver ===================
Size LDA Align. Time(s) GFlops Residual Residual(norm) Check
5000 5000 4 0.748 111.4607 2.384642e-011 3.325192e-002 pass
5000 5000 4 0.743 112.2020 2.384642e-011 3.325192e-002 pass
5000 5000 4 0.750 111.1514 2.384642e-011 3.325192e-002 pass
5000 5000 4 0.769 108.4265 2.384642e-011 3.325192e-002 pass
5000 5000 4 0.753 110.7182 2.384642e-011 3.325192e-002 pass
Performance Summary (GFlops)
Size LDA Align. Average Maximal
5000 5000 4 110.7918 112.2020
実行結果(Standard 1GB Benchmark)
Maximum memory requested that can be used=800204096, at the size=10000
=================== Timing linear equation system solver ===================
Size LDA Align. Time(s) GFlops Residual Residual(norm) Check
10000 10000 4 5.776 115.4480 1.020314e-010 3.597732e-002 pass
10000 10000 4 6.063 109.9938 1.020314e-010 3.597732e-002 pass
10000 10000 4 6.063 109.9856 1.020314e-010 3.597732e-002 pass
10000 10000 4 6.074 109.7905 1.020314e-010 3.597732e-002 pass
10000 10000 4 6.116 109.0323 1.020314e-010 3.597732e-002 pass
Performance Summary (GFlops)
Size LDA Align. Average Maximal
10000 10000 4 110.8500 115.4480
実行結果(Extended 1.5GB Benchmark)
Maximum memory requested that can be used=1613408096, at the size=14200
=================== Timing linear equation system solver ===================
Size LDA Align. Time(s) GFlops Residual Residual(norm) Check
14200 14200 4 16.920 112.8397 1.815724e-010 3.187790e-002 pass
14200 14200 4 17.245 110.7170 1.815724e-010 3.187790e-002 pass
14200 14200 4 17.285 110.4605 1.815724e-010 3.187790e-002 pass
14200 14200 4 17.332 110.1583 1.815724e-010 3.187790e-002 pass
14200 14200 4 17.250 110.6798 1.815724e-010 3.187790e-002 pass
Performance Summary (GFlops)
Size LDA Align. Average Maximal
14200 14200 4 110.9711 112.8397
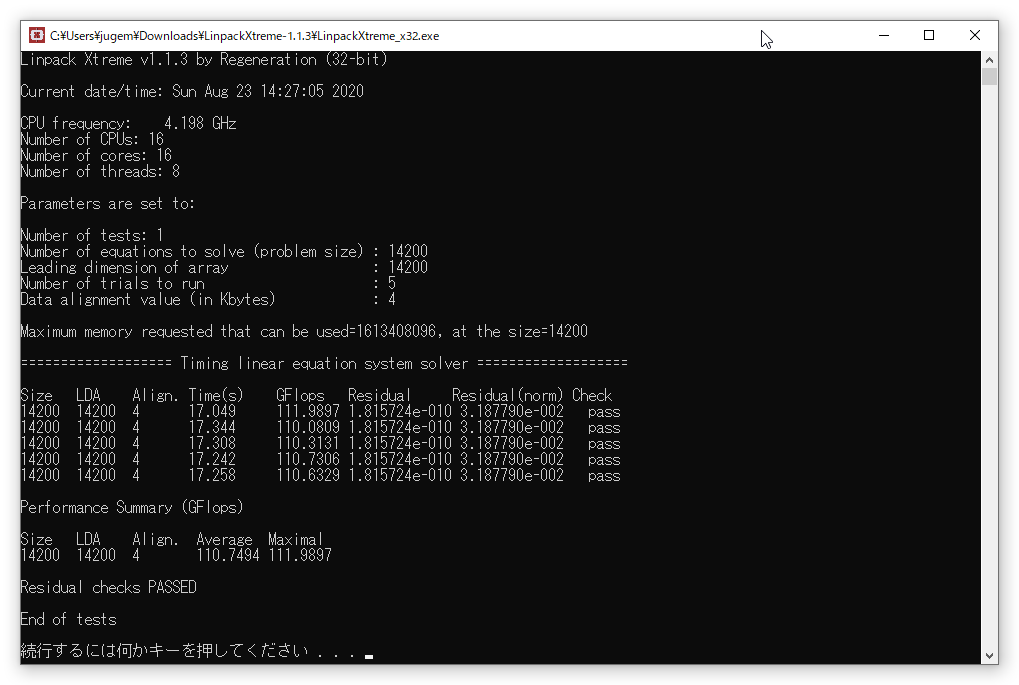
実行結果を比較する
今回の実行結果の最高値は115.4GFlopsでした。8コアCPUなので、1コアあたりの性能はおよそ14.4GFlopsとなります。一方、富岳は1ノードあたり48コア構成×158,976ノード=7,630,848コアで415.5PFlops。1コアあたり54.4GFlopsとなり、ノートPCでの実行性能の3倍以上となりました。
まとめ
実行結果は納得の結果ですね。そして、これを760万個も束ねて動作させてる富岳は凄すぎると改めて実感しました。今回テストできなかった実装、lu2についても引き続き調べてみたいと思います。